Cryptography vs Cryptocurrency – one enabling the other

For many, the word ‘crypto’ brings Lamborghini’s, neckties with Bitcoin signs printed on them or really bad hip-hop, but up until some years ago, the original meaning was not crypto-currency, but cryptography. That is also the topic of this blogpost. Consider it a gentle introduction into a very specific branch of cryptography – zero-knowledge proofs (or ZKP) – and why blockchain has helped bring them back into vogue.

What are ZKP – intuition

So, let’s start off with the basics, what are zero-knowledge proofs? I’ll explain it through three common analogies with varying complexity, they all describe the same concept but appeal to different audiences.

1. This analogy is from StackExchange. Imagine your friend, Alice, tells you that she has a super-power. An amazingly useless super-power, but still. She can count all the leaves on a tree in your garden in front of your house in a few seconds! Of course, you don’t believe her, so you ask Alice to prove it. We’ve now created two roles that are omnipresent in ZKP, a prover (your friend Alice) and a verifier (you in this case). She proposes that she closes her eyes, you can then choose to either remove a leaf from the tree or not, and finally she can open her eyes. Now, to prove her super-power, she has to tell you whether or not you removed a leaf from the tree. If she’s wrong she failed to prove anything, but if Alice is right, you realise that she had a 1/2 chance to guess correctly and was just lucky. So you repeat the experiment, now if she’s right again, she would have had to have been right two times in a row, meaning her odds of being guessing correctly were 1/4. (At least assuming independence of events). This goes on and on until you are sufficiently convinced of her super-power being real. In this scenario, you didn’t learn HOW she does her magic counting of leaves, but you’re very sure that she know how to do it. There was ZERO KNOWLEDGE transferred from Alice to you regarding the procedure itself. Additionally, there was no, or a very small possibility for you, being honest, of not believing in Alice’s capability, and she couldn’t have convinced you without actually having the super-power. These three criteria are called ‘zero-knowledge’, ‘completeness’ and ‘soundness’, respectively, and are a part of all ZKP.

2. This one is from the booklet “Applied Kid Cryptography or How To Convince Your Children You Are Not Cheating” by Naor, Naor and Reingold. It relies on the game called “Where’s Waldo?” or “Where’s Wally?” in the UK-version. The goal of the game is to find the image of Waldo on a page filled with other things and figures. Let’s assume Alice and yourself are playing this game together. All of a sudden, Alice exclaims “I found Wally!”. Aggravated with jealousy you scream out “So prove it!”, (first the revelation of the leaf-counting super-power and now this!?). So how can Alice prove her knowledge of where Waldo is, without revealing to anyone else where he is? Simple, she takes a big cardboard with only a cut-out in the middle, just the size of a Waldo-image. As you close your eyes, Alice places the cardboard over the open pages of the Where’s Waldo?-book exactly so that only Waldo can be seen through the cut-out. You can verify that Alice knew where Waldo is, without learning where on the page he is. Again, this satisfies our three properties of zero-knowledge, completeness (you have to believe Alice found Waldo given the information she presented to you) and soundness (Alice couldn’t cheat by randomly placing the cardboard on the book except by being extremely lucky).

3. Now, my favourite example from a highly recommended blogpost by Jeremy Kun is more in the theoretical space. Instead of a difficult problem like counting leaves or finding Waldo, we now have the provably difficult and more formally defined problem of proving that two graphs are isomorphic. Let’s unpack that:

– A graph, G, is defined by a number of edges connecting the vertices of the graph. Thus a graph G = (V,E)
– Each edge can be represented as the tuple (u,v), where u and v are integers between 1 and the number of vertices of G, n.
– Given two graphs G = (V,E) and G’ = (V’,E’), they are isomorphic if there exists a couple of functions f: V->V’ and g: E->E’ such that f associates each value in V with exactly one element in V’ and vice versa. Correspondingly, g associates each value in E with exactly one value in E’ and vice versa.

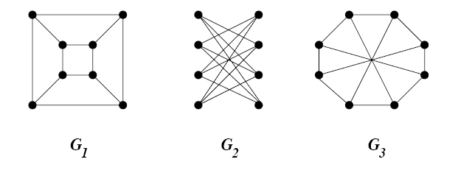
source: Jeremy Kun’s blog on Math and Programming – https://jeremykun.files.wordpress.com/2015/11/gi-example.png?w=587&zoom=2

Intuitively, this means that graphs are isomorphic if we can transform one into the other by simply moving around the vertices, not adding or removing any edges and ending up with two identical figures. This is not exactly rigorous, but still somewhat accurate for our purposes.

Now, for the zero-knowledge part! Given two graphs, there’s no easy or efficient way of finding out if they are isomorphic. (If you find a way, let me know.) So, let’s say Alice knows that there exists an isomorphism between them, but she doesn’t want to reveal her isomorphism to you. She does this by taking e.g. G and mixing V. Then she sends you her newly formed isomorphic graph, called H. Alice additionally saves the permutation she did on G for later.

After having received H, you flip a coin with equal probabilities and depending on the outcome you give Alice a challenge. Heads, and Alice should provide you with the inverse, or backwards, permutation which gave her H. It should then give you G. If tails, Alice should provide you with her secret isomorphism, f composed with the permutation. This should now give you G’ when applied to H.

Given either of those permutations, you should now be able to verify that Alice possesses a ‘secret’ isomorphism. Additionally, you haven’t learned anything about the solution since you only received a uniformly random permutation or two uniformly random permutations composed which gives another uniformly random permutation.

Why ZKPs are interesting to blockchain

Ok, now that we’ve understood a bit what ZKP means, let’s see why it is interesting for blockchain technology. The most obvious area of application is of course privacy. Being able to prove something without having to reveal any information about the subject sounds like utopia for almost everyone with an eye on the current state of affairs in big data applications of corporates and states. A second, less obvious type of application is for scaling in blockchains. This relies on the fact that a proof of knowledge can be more succint, from a storage point of view, than the information it’s proving. Let’s look at some use cases of both application areas in more detail:

One of the first live applications of ZKP in blockchain for privacy was by ZCash – a cryptocurrency where the ‘knowledge’ being proven is that the sum of outgoing transactions are equal to the sum of incoming transactions (ZCash uses a UTXO model), that the sender has the authority to spend the coins being sent and finally that the private keys of the incoming ‘notes’ are effectively locking the whole transaction from being modified without the keys in question.

Another use case of ZKP for privacy is by Sovrin, who mainly uses regular public key cryptography and a fairly clever protocol to issue verifiable credentials such as “possession of a valid driver’s license in EU”. Then they apply a type of ZKP called accumulators to prove non-revocation of that very credential in a very succint manner. This was initially researched by IBM in the so-called idemix, back in 2007, but lacked an adequate platform to store the non-revocation lists in a persistent, trustless manner. Until blockchain arrived.

Generally speaking, ZKP can be used for a wide range of privacy-preserving applications, especially when it comes to the topic of identity, things such as range-proofs whereby it can be proven that one’s age is within a certain range (e.g. 18-65) without revealing the actual age. Or it can be proven that one is a resident of the EU without revealing in which country exactly.

One of the most pressing issues of public blockchains these days (and admittedly since some time) is that of scalability. Interestingly, ZKP may have a solution for this. Like ZCash, another privacy-focused cryptocurrency Monero implemented ZKP. However, Monero was using a different algorithm called RingCT to hide transaction information. It didn’t rely on the often criticised ‘trusted setup’ of ZCash (more here) but therefore had a very large transaction size resulting in low throughput. This was improved greatly by the application of so-called bulletproofs (also a type of range-proofs actually) in October 2018. This meant that the average transaction size was reduced by at least 80%, and the fees accordingly.

Even more extreme measures are being built by the coda team who aim to recursively compress an entire blockchain into a 20kB ZKP. Their CTO Izaak Meckler called it “A picture of a picture of a picture of a picture.”. It works by using a ZKP to prove the knowledge of a ZKP, which proves the knowledge of a ZKP, etc. This effectively leads to a constant-size blockchain which can be verified by anyone easily, not like in many existing public blockchains where the more users a blockchain has, the more difficult it gets for the average user to verify. Coda does, interestingly, not use ZKP at all for privacy. Yet.

We’ve seen a few examples to intuit what ZKP means and why they are interesting to apply in blockchain technology. It is part of what we are working on at Datarella, implementing industrial blockchain solutions for clients and in RAAY. If you would like to dig deeper into some of the topics we’ve learned about today, here are some resources:

– https://jeremykun.com/2016/08/01/zero-knowledge-proofs-for-np/
– https://z.cash/technology/
– https://www.youtube.com/watch?v=DfEG5nhMRyQ&list=PLj80z0cJm8QHvg1ydi6rTEUK1SpxbtKnM
– https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6
– https://www.uow.edu.au/~bmaloney/wuct121/GraphsWeek10Lecture2.pdf
– https://zokrates.github.io/
– https://medium.com/aztec-protocol/how-to-code-your-own-confidential-token-on-ethereum-4a8c045c8651